Exerciții de vorbire:
Rudolf Steiner: A se exersa învățându-le pe de rost!
Din: „Găsit-am o cărare” de Christian Morgenstern [Nota 38]:
T. caută să explice în mod vizual, pentru copiii de nouă ani, noțiunea de suprafață (a decupa pătrate pentru măsurarea ariei unor pătrate mai mari, șablonizare).
Rudolf Steiner: Este bine să-i facem să înțeleagă că atunci când avem o latură a pătratului cu o lungime de 3 m, suprafața este de 9 m2, dar cu aceasta rămânem tot în sfera care compune ceva din niște piese grafice și va fi foarte greu, totuși, să facem ca aici să ia naștere o reprezentare justă despre arie.
Eu m-am referit la aceasta: Cum procedăm în mod just și la ce vârstă se poate găsi un astfel de procedeu, prin care să aflăm, într-adevăr, că aria e arie și că ea devine arie atunci când înmulțim lungimea cu lățimea? Cum ajungem să facem să ia naștere în copil această noțiune a ariei? ‒ Acest lucru depinde de locul unde plasăm orele consacrate ariei. Trebuie să spunem: Nu e bine să plasăm aceste ore înainte de a fi început socotitul cu litere. Putem face o predare rațională a problemelor ariei abia după ce am început calculul algebric. Așa că răspunsul este: Așteptăm cu orele despre arie până când am început calculul algebric.
Și acum, întrebarea: Cum faceți trecerea cu copiii de la socotitul obișnuit cu cifre la socotitul cu litere? Vreau să vă arăt drumul pe care să apucați, iar dvs. îl veți dezvolta în continuare. Înainte de a trece la socotitul cu litere, trebuie să fi parcurs cu copiii calcularea dobânzilor: dobânzile sunt egale cu capitalul înmulțit cu procentul, înmulțit cu timpul, împărțit la 100.
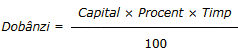
Dacă prescurtăm, folosind doar inițialele, putem scrie:
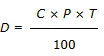
T = tempus, în latină = timp, este prescurtarea cel mai des folosită pentru cuvântul timp.
Când ajungeți la această formulă, porniți de la niște numere obișnuite și copilul va înțelege relativ ușor ce e capitalul, care sunt procentele, care e timpul ș.a.m.d.
Așadar, veți căuta să explicați copilului acest proces și veți căuta să vă convingeți dacă majoritatea copiilor au înțeles. Și de aici veți trece la formula de mai sus și veți avea mereu grijă să existe o regulă.
C = capital; P = procent; T = timp (tempus); D = dobânzi. Atunci, ceea ce am dat mai sus este o formulă pe care o țin minte doar ca formulă de bază.
În acest fel am făcut deja primul pas al trecerii la socotitul cu litere. Dacă elevul are acum această formulă, nu trebuie decât să introducă numărul în această formulă și trebuie să iasă întotdeauna rezultatul corect. Dacă aveți apoi formula derivată de aici:
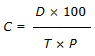
se poate ține minte pe cale memorativă faptul că putem schimba între ele cum vrem cele trei litere C, P, T, astfel încât mai rezultă următoarele posibilități:

În acest fel l-am învățat pe copil calcularea capitalului și acum putem trece la socotitul cu litere. Puteți spune liniștiți: „Noi am învățat că o sumă oarecare 25 a fost egală cu 8 plus șapte plus 5 plus 5; 25 = 8 + 7 + 5 + 5;” Nu-i așa, acest lucru l-a înțeles copilul deja mai înainte. Acum, după ce i-ați arătat asta, îi puteți spune: „Aici (în locul lui 25), poate să fie și altă sumă, iar aici, în loc de 8, 7, 5, 5, pot fi alte numere, așa că putem spune și că aici se află un număr «oarecare». Așadar, aici se află, de pildă: S, o sumă. Iar aici: a + b + c + c. Dar, dacă aici avem c în locul primului 5, el trebuie să stea și în locul celui de-al doilea 5. Întocmai așa cum în locul unui capital oarecare scriem c, pun în acest loc litera c.”
După ce ați arătat într-un caz concret trecerea de la număr la literă, puteți dezvolta acum și noțiunea de înmulțire, și din acest 9 × 9 concret puteți dezvolta a × a. Sau puteți dezvolta din 9 × 12 pe a × b ș.a.m.d. Așadar, aceasta ar fi calea de a trece de la aceste socoteli cu numere la socotitul cu litere. Și de aici, la calcularea ariei, a × a = a2.
Temă pentru mâine: Să dezvoltați într-un mod cât mai clar și ușor de înțeles pentru copiii de unsprezece, doisprezece ani, calcularea dobânzilor, cu tot ceea ce ține de aceasta, cu inversare: calcularea procentelor, a timpului, a capitalului. ‒ Pornind de aici, dezvoltați apoi felul cum explicăm calcularea scontului. Apoi, felul cum îl facem pe copil să înțeleagă calcularea rabatului și a ambalajului, si cum îl învățăm noțiunea de schimb și calcularea acestuia. Aceste lucruri țin de vârsta de doisprezece, treisprezece ani; dacă se învață acum, rămân pentru întreaga viață, altfel le uităm mereu. O putem face într-un mod simplu, dar aici îi e locul. Dacă un om știe să facă aceste lucruri așa cum trebuie, el stăpânește metodica întregii aritmetici. Calcularea dobânzii dobânzilor nu ține de această vârstă.
Așadar, o trecere organică la socotitul cu litere până la înmulțire și, de aici, la calcularea ariei.
V-aș ruga acum să ne ocupăm de celelalte întrebări puse ieri. Căci și aici este important să stimulăm prezența de spirit a copiilor prin niște situații concrete în care îi punem să efectueze calcule.
G. propune să se organizeze un mic stand de vânzare cu fructe, legume, cartofi ș.a.m.d., copiii cumpărând, vânzând, dând rest singuri, calculând totul singuri.
Rudolf Steiner: Acest principiu negustoresc este foarte bun pentru clasa a II-a. Și e bine să se insiste ca acela căruia i-am dat de făcut o socoteală, s-o și facă și să nu admitem să o facă alt copil în locul lui. Să menținem mereu treaz interesul tuturor!
Se vorbește despre socotitul din cap; despre socotitul care nu recurge la ajutorul scrisului.
Rudolf Steiner povestește că Gauß [Nota 39], pe când avea șase ani, a ajuns o dată la următoarea rezolvare: I se dăduse sarcina de a aduna numerele de la 1 până la 100. Gauß s-a gândit că e mai avantajos și mai simplu de ajuns la rezultat dacă luăm încă o dată aceleași numere, dar le ordonăm lângă prima serie de la 1 la 100, în așa fel încât să ne putem reprezenta prima serie ca de obicei, scrisă de la stânga la dreapta: 1, 2, 3, 4, 5, ... 100, dar sub ea, în ordine inversă, scrisă a doua: 100, 99, 98, 97, 96, ... 1, astfel încât sub 1 stă 100, sub 2 ‒ numărul 99, sub 3 numărul 98. Atunci, cele două numere scrise unul sub altul ar da de fiecare dată suma 101. Suma trebuie luată de o sută de ori, dă 10.100 și ea trebuie apoi împărțită la 2 ‒ pentru că am adunat de două ori numerele de la 1 la 100, o dată în ordine crescătoare, o dată în ordine descrescătoare ‒ rezultă 5.050. În acest fel a rezolvat pe atunci Gauß, din cap, spre mirarea nu mică a învățătorului său, acest exercițiu.
T. citează, printre alte două feluri de exerciții, următoarele: 1. calcularea timpului și a segmentelor, când sunt date locomotive cu un diametru al roților diferit; 2. exerciții cu umplerea și golirea unor butoaie prin conducte de scurgere de diametre diferite.
Rudolf Steiner: Pentru născocirea exercițiilor de aritmetică putem apela la fantezie. Putem dezvolta prezența de spirit prin exerciții de mișcare. Puteți trece la practică prin exercițiul de ieri, dacă spuneți: Am trimis un mesager cu o scrisoare. Scrisoarea nu mai e valabilă. Trebuie să trimit alt mesager. Cât de repede trebuie să înainteze acesta, ca să sosească înainte ca prima scrisoare să provoace o nenorocire? Copilul trebuie să poată socoti acest lucru măcar aproximativ; asta e foarte bine.
Un participant atrage atenția asupra unor calcule greșite.
Rudolf Steiner: Asemenea calcule greșite sunt foarte obișnuite. Este ceva obișnuit să se ia în calcul și greșelile. Ei bine, va trebui să facem astăzi undeva o asemenea socoteală greșită și ea va trebui corectată cândva. Când Copernic și-a alcătuit „sistemul copernician”, el a stabilit trei principii. Dacă s-ar folosi toate trei pentru a se schița mersul Pământului prin Cosmos, s-ar obține o cu totul altă mișcare decât cea presupusă acum de astronomii noștri și învățată în școlile noastre. Această mișcare eliptică devine posibilă numai dacă se face abstracție de cel de-al treilea principiu. Dacă astronomul își îndreaptă telescopul spre depărtările cerești, lucrurile nu se potrivesc. În acest scop, sunt luate în calcul și greșelile; prin ecuațiile lui Bessel, sunt luate în calcul, în fiecare an, greșelile pentru ceea ce nu se adeverește în realitate. În ecuațiile lui Bessel care iau în calcul greșelile se află și al treilea principiu al lui Copernic.
Din punct de vedere metodologic, trebuie să procedăm în așa fel încât să nu-l facem pe copil să se ocupe doar de niște exemple născocite, ci să ajungem la exemple practice din viață. Trebuie să facem în așa fel încât totul să ducă în cele din urmă la viața practică. Putem face întotdeauna ca ceea ce vine mai târziu să fertilizeze ceea ce a fost mai înainte, și invers.
Unde ați face să se ajungă cu toate aceste calcule ale mișcărilor, cu scurgerea lentă a lichidelor prin deschizături mici, cu scurgerea lor rapidă prin deschizături mari, cu exercițiile mișcării circulare la mașini cu roți de mărimi diferite ‒ unde ați face să ducă toate acestea?
Cel mai bine ar fi să treceți la explicarea ceasului în diferitele lui forme, ca pendulă, ceas de buzunar ș.a.m.d.
Teme pentru mâine:
Mai întâi: Tratarea unei teme de istorie, după modelul dat mai înainte, din punctul de vedere al istoriei culturii și civilizației.
În al doilea rând: Tratarea unui lucru oarecare din natura generală, răsăritul și apusul Soarelui, anotimpurile ș.a.m.d., ceva care vă este la îndemână, ceva din edificiul lumii. Esențialul este să scoateți în evidență metoda de predare.
În al treilea rând: Despre principiile muzicale în primul an de școală.
În al patrulea rând: Ce formă să dăm elementului poetic în limbile engleză și franceză? Cum să-i deprindem pe copii să simtă elementul poetic din limba engleză, din limba franceză?
În al cincilea rând: Cum putem sa-l învățăm pe copil noțiunea de elipsă, hiperbolă, cerc, lemniscată și noțiunea de loc geometric? ‒ Toate acestea trebuie să fie transmise copiilor înainte ca ei să părăsească școala.